Before the Academy Awards (the Oscars) are handed out to each year’s winners, movie stars walk the red carpet. They pose for photos and are interviewed. On February 9, 2020, one young actress brought a black knight with her. This article explains why, and then presents a chess problem, from Grandmaster John Nunn’s most recent book, which features a black knight.

Ten-year-old Julia Butters had a role in Quentin Tarantino’s Once Upon a Time in Hollywood. Here is one of Julia’s interviews from the red carpet. In that video, pay attention from 1:50 onwards, where she says, “This chess piece is very important to me because Quentin actually gave this to me. And he has the king, of course. He says, ‘I’m the king, you’re the knight, deal with it.’‘”
While Tarantino may have been the king during the filming of Once Upon a Time in Hollywood, for his previous film, The Hateful Eight, Tarantino saw himself the player in charge of all the chessmen. In a 2015 interview about The Hateful Eight, Tarantino stated, “You don’t know when the violence is going to happen, but you know it is going to happen, and you are just waiting for it. The trick was extending that for the entire movie. If the movie works, it should be suspenseful. There is a long, long buildup as I put my chess pieces in place. I am playing chess, and I have to put them all in the right spot before I start killing them off, and I am asking you for some patience.”

In the following chess problem, you could imagine the black knight as Julia Butters and the black king as Quentin Tarantino. Or you could imagine all the problem’s chessmen as actors in Tarantino’s next film. The problem is from John Nunn’s Chess Endgame Workbook for Kids, published in 2020 by Gambit Publications.
When I first looked at this problem, I felt panic rather than the patience Tarantino requested. John Nunn’s hint was “How can Black draw?” but how can my black knight get to the “right spot” where it could kill itself while killing the white pawn?
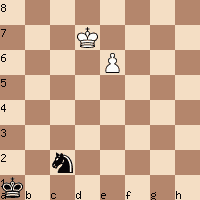
(Click here to practice this problem yourself)
Then I thought, wait, what if I can fork the white king and the queen (which the pawn will promote to) in a couple of moves? Once I had that idea, I knew exactly where the black knight must move. Nunn’s answer explains both my initial error (trying to capture the pawn by moving to a rank close to it) and the solution (looking for a fork after the pawn has promoted). Nunn gives 1…Ne3! as the solution, followed by 2. e7 Nd5 Not 2…Ng4? 3. Ke6 preventing the N from getting to f6. With the text move, 2…Nd5, the black knight threatens to capture the e7-pawn and draw instantly. Therefore, White has to try promoting. 3. e8(Q) Nf6+, forking the newly-minted Q on e8 and the K on d7. Then, of course, the N will give itself up for the Q with 4. K anywhere Nxe8. A mistake would have been 1…Nd4? because after 2. e7 there is no way to catch the pawn. Thus, even though visually 1…Nd4 moves the knight closer to the e-pawn, the further-away move 1…Ne3 is correct.